Mastering The Angle Of Hexagon: A Guide To Geometry's Hidden Gem

The angle of a hexagon is an intriguing aspect of geometry that captures the attention of both beginners and experts alike. With its symmetrical beauty and practical applications, the hexagon stands as a testament to the wonders of mathematics. Whether it's in the structure of honeycombs or the design of tiles, understanding the angles of a hexagon opens up a world of geometric exploration.

Hexagons are six-sided polygons that play a significant role in various fields, from architecture to nature. Each angle of a hexagon holds unique properties, contributing to the overall harmony and balance of the shape. This article delves into the fascinating world of hexagonal geometry, exploring the intricacies of its angles and uncovering the secrets behind its widespread use.

As we journey through the angles of a hexagon, we'll uncover the mathematical principles that govern this shape, examine its real-world applications, and answer common questions about its properties. With a focus on clarity and accessibility, this guide aims to provide a comprehensive understanding of the angle of hexagon for readers of all backgrounds.

Read also:

Khal Drigo The Charismatic Leader And His Enduring Influence

Table of Contents

• What is a Hexagon?
• Understanding the Angle of Hexagon
• Types of Hexagons
• Calculating the Angle of Hexagon
• Why are Hexagons Important?
• Real-World Applications
• Examples in Nature
• Hexagons in Architecture
• Hexagons in Technology
• Frequently Asked Questions
• Conclusion

What is a Hexagon?

A hexagon is a polygon with six sides and six angles. It is one of the most common shapes in nature and human-made structures. Each of the six sides is equal in length in a regular hexagon, and all internal angles are equal. The hexagon is a versatile shape, often used in tiling patterns due to its ability to tessellate perfectly without any gaps.

Characteristics of a Hexagon

Hexagons possess several distinctive characteristics:

• Six sides and six vertices
• Internal angles sum up to 720 degrees
• Can be regular (all sides and angles are equal) or irregular
• Symmetrical shape with rotational symmetry of order 6

Understanding the Angle of Hexagon

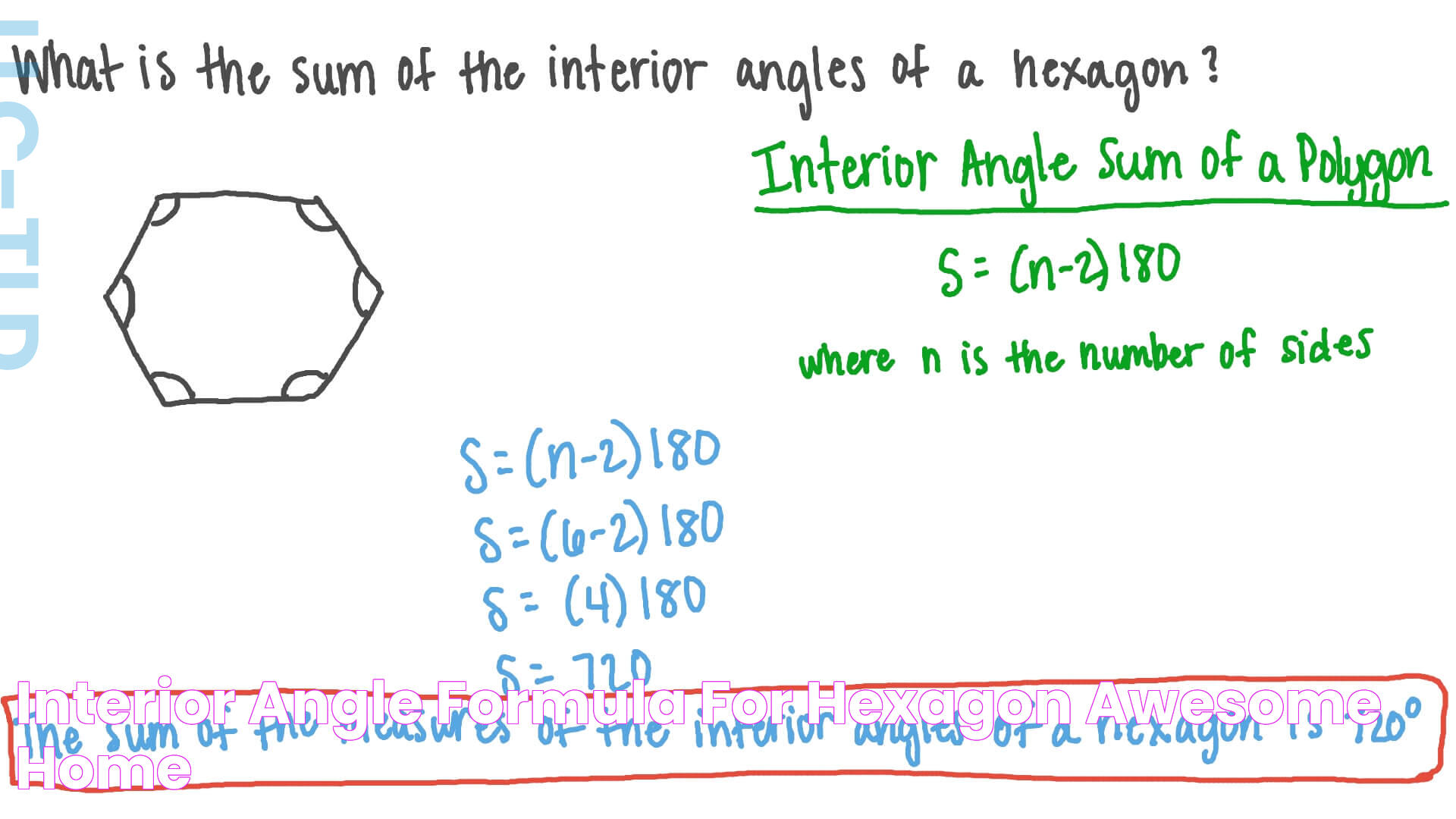
The angle of a hexagon, particularly in a regular hexagon, is a crucial aspect of its geometry. Each internal angle in a regular hexagon is 120 degrees. This property is derived from the formula for calculating the internal angles of a polygon, which is:

Internal Angle = [(n-2) × 180°] / n, where n is the number of sides.

For a hexagon, this calculation yields:

Internal Angle = [(6-2) × 180°] / 6 = 120°

Read also:

Essential Guide To Job And Family Services Support Resources And Opportunities

Why is the Angle of Hexagon Significant?

The angle of a hexagon is significant for several reasons:

• It allows for perfect tessellation, making it ideal for tiling and partitioning spaces
• Its symmetry provides structural stability in both natural and engineered forms
• The uniformity of angles aids in simplifying calculations in geometry and design

Types of Hexagons

Hexagons can be classified into two main types: regular and irregular hexagons. Understanding these types helps in recognizing the versatility of hexagonal shapes in different contexts.

Regular Hexagons

A regular hexagon has all sides of equal length, and all internal angles are equal to 120 degrees. This uniformity allows it to tessellate without gaps, making it a popular choice in design and architecture.

Irregular Hexagons

Irregular hexagons have sides and angles that are not equal. While they may not tessellate as perfectly as regular hexagons, they offer flexibility in design and can be found in various artistic and architectural applications.

Calculating the Angle of Hexagon

Calculating the angle of a hexagon involves understanding both its internal and external angles. While the internal angles of a regular hexagon are straightforward, calculating angles in irregular hexagons requires more complex geometric principles.

Internal Angles

The sum of internal angles in any hexagon is always 720 degrees, regardless of whether it is regular or irregular. This can be derived from the general formula for the sum of internal angles in a polygon, which is:

Sum of Internal Angles = (n-2) × 180°, where n is the number of sides.

External Angles

External angles in a hexagon are the angles formed between one side of the hexagon and the extension of an adjacent side. For any polygon, the sum of the external angles is always 360 degrees. In a regular hexagon, each external angle is 60 degrees.

Why are Hexagons Important?

Hexagons are important due to their unique properties and versatility. Their ability to tessellate perfectly makes them ideal for various applications, from architecture to biology.

Benefits of Hexagonal Structures

• Efficient use of space: Hexagons fill a plane with no gaps, maximizing the use of space in designs.
• Structural strength: The symmetrical nature of hexagons contributes to their stability and resilience.
• Natural occurrence: Hexagons frequently occur in nature, offering inspiration for sustainable design solutions.

Real-World Applications

Hexagons are found in numerous real-world applications, showcasing their practicality and aesthetic appeal. From nature to technology, hexagonal shapes are utilized for their efficiency and functionality.

Engineering and Construction

In engineering, hexagonal designs are used to create strong and lightweight structures. The honeycomb structure, inspired by the natural hexagon, is a popular design in the aerospace and automotive industries due to its strength-to-weight ratio.

Design and Aesthetics

Hexagons are often used in design for their visually appealing symmetry. They are common in tiling patterns, jewelry design, and even in the layout of urban spaces, providing both functionality and beauty.

Examples in Nature

Nature is full of examples of hexagonal patterns, demonstrating the efficiency and beauty of this geometric shape. From the microscopic to the astronomical, hexagons appear in various natural phenomena.

Honeycombs

Perhaps the most famous example of hexagons in nature is the honeycomb. Bees construct their hives using hexagonal cells, which provide maximum storage with minimal material use.

Giant's Causeway

The Giant's Causeway in Northern Ireland features naturally occurring hexagonal basalt columns formed by volcanic activity. This geological wonder highlights the hexagon's presence in Earth's natural formations.

Hexagons in Architecture

Architects often incorporate hexagonal designs in their projects due to the shape's stability and aesthetic appeal. Hexagons provide structural integrity and a modern appearance to buildings and spaces.

Modular Design

Hexagons are used in modular architecture to create flexible and sustainable living spaces. The shape's ability to tessellate allows for easy expansion and adaptation of structures.

Decorative Elements

Hexagonal motifs are popular in decorative architecture, such as flooring, wall panels, and facades. Their geometric symmetry adds a contemporary touch to both interior and exterior designs.

Hexagons in Technology

Technology harnesses the power of hexagons in various ways, from data visualization to nanotechnology. The shape's efficiency and symmetry provide numerous advantages in technological applications.

Data Visualization

Hexagonal grids are used in data visualization tools to represent complex data sets. The shape's uniformity allows for clear and concise representation of information.

Nanotechnology

In nanotechnology, hexagons are used to create strong and lightweight materials, such as graphene. The hexagonal lattice structure of graphene contributes to its exceptional strength and electrical conductivity.

Frequently Asked Questions

What is the sum of internal angles in a hexagon?

The sum of internal angles in any hexagon is 720 degrees.

How does a hexagon tessellate?

A regular hexagon tessellates perfectly with no gaps due to its equal sides and angles, fitting together seamlessly.

Why do bees use hexagonal shapes in honeycombs?

Bees use hexagonal shapes in honeycombs because they provide maximum storage space with minimal material, optimizing efficiency.

Can hexagons be irregular?

Yes, hexagons can be irregular, meaning their sides and angles are not equal, offering flexibility in design.

What are some examples of hexagons in nature?

Examples of hexagons in nature include honeycombs, the Giant's Causeway, and certain crystal formations.

How are hexagons used in technology?

Hexagons are used in technology for data visualization, nanotechnology materials, and efficient design structures.

Conclusion

The angle of hexagon is a fundamental aspect of geometry that reveals the beauty and efficiency of this shape. From its perfect tessellation to its presence in nature and technology, hexagons demonstrate their versatility and appeal. Understanding the angles of a hexagon provides valuable insights into the world of mathematics and its practical applications. Whether you're a student, designer, or simply a curious mind, exploring the angle of hexagon opens the door to a deeper appreciation of geometric wonders.