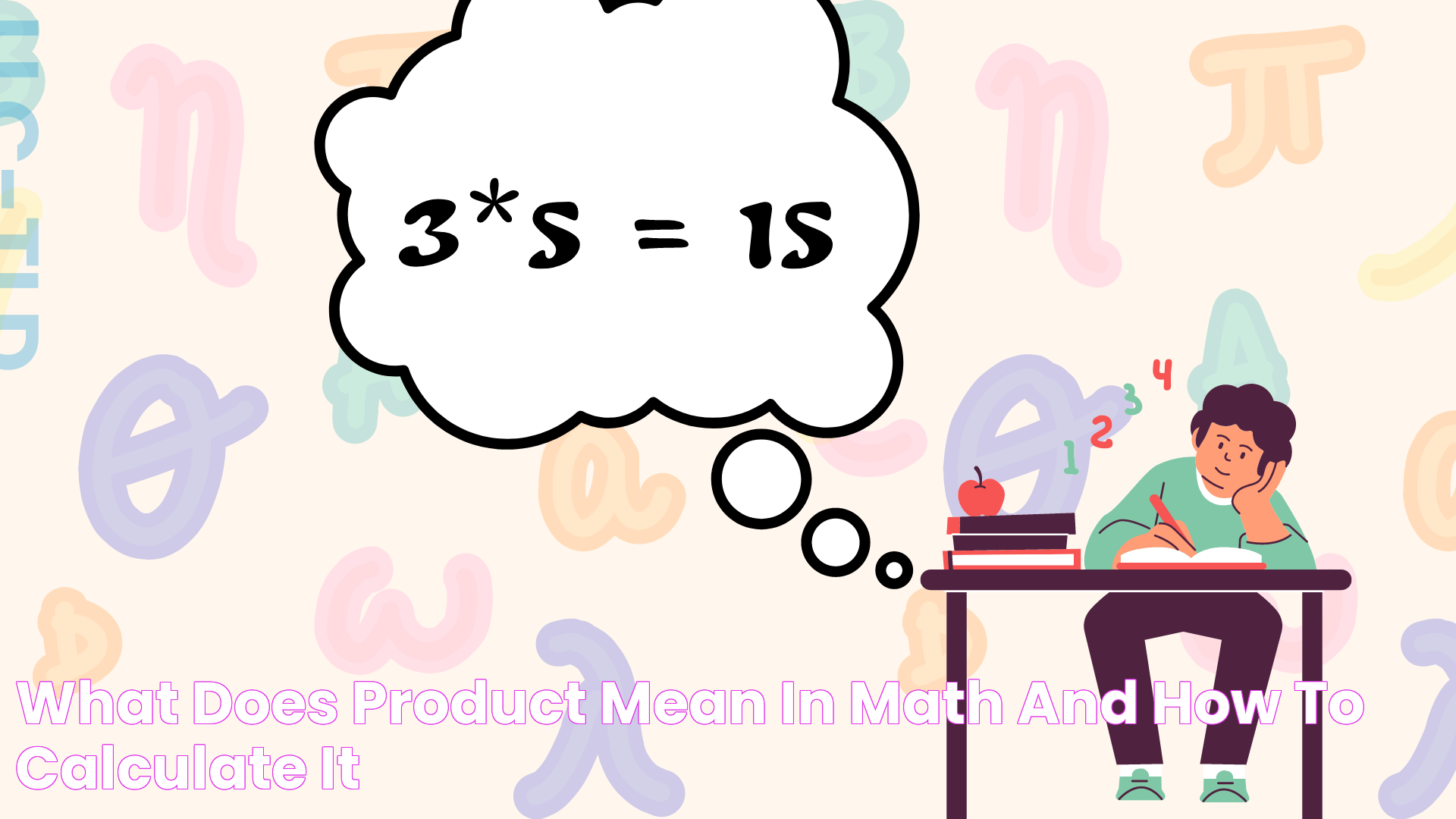Essential Guide To Product In Math: Definition, Applications, And More

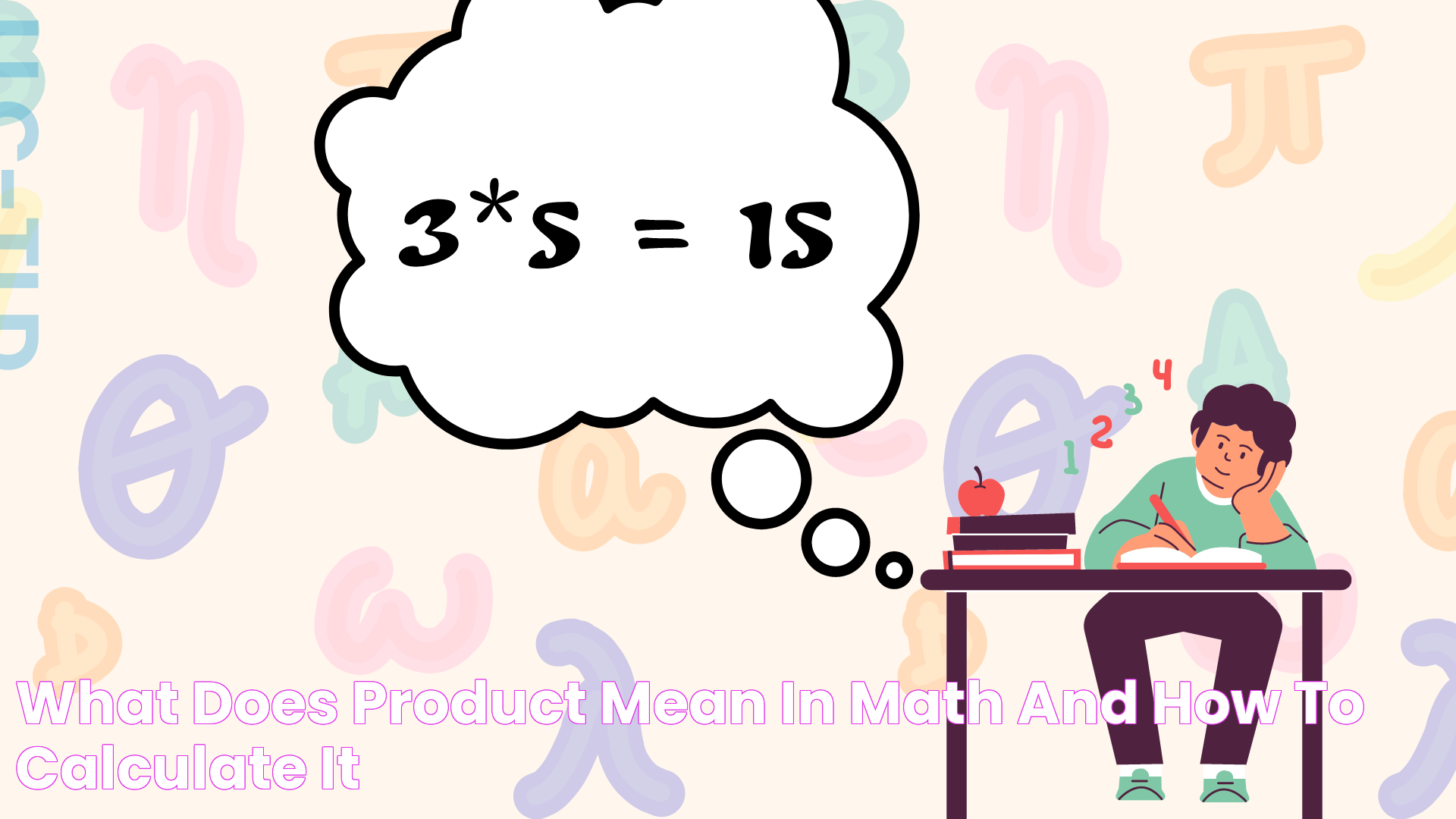
The concept of a product is fundamental to mathematics, yet its meaning may vary slightly depending on the context. In its most basic form, a product represents the result of multiplying two or more numbers together. This operation is one of the core arithmetic operations, alongside addition, subtraction, and division. Understanding the product is crucial not only for basic calculations but also for more advanced mathematical concepts and real-world applications.

The term 'product' in mathematics is derived from the Latin word 'productum,' which means 'to lead forward' or 'to bring forth.' This etymology reflects how the product brings together different numbers to create a single result. However, the significance of the product extends beyond simple arithmetic. In algebra, the product of variables can represent complex relationships, whereas in geometry, it can describe the area or volume of shapes. Thus, the product serves as a bridge between various branches of mathematics, providing a cohesive understanding of numbers and their interactions.

In everyday life, the product is a versatile tool used in numerous situations. From calculating expenses and budgeting to understanding scientific measurements and engineering calculations, the concept of a product is omnipresent. By mastering the notion of products, individuals can enhance their problem-solving skills and deepen their appreciation for the intricacies of mathematics. This article delves into the multifaceted nature of the product in math, exploring its definition, properties, types, and applications in a structured and comprehensive manner.

Read also:

Snapgod Izzy S A Deep Dive Into The Life And Legacy

Table of Contents

• Definition of Product in Math
• Properties of Product
• Types of Products in Mathematics
• How is Product Used in Math?
• Examples of Product in Mathematics
• Importance of Product in Real Life
• Product in Algebra
• What Does Product Mean in Math Geometry?
• Product in Calculus
• Common Misconceptions About Product
• Product in Computer Science
• Product in Economics and Business
• Historical Perspective of Product
• Frequently Asked Questions
• Conclusion

Definition of Product in Math

The term 'product' in mathematics refers to the result obtained from multiplying two or more numbers. In the simplest terms, if you multiply the numbers 4 and 5, the product is 20. The concept is straightforward in basic arithmetic but can become more complex when involving variables, polynomials, matrices, or vectors. Fundamentally, the product is a means of combining quantities to produce another quantity that represents their combined magnitude.

To understand the product's role in more advanced mathematics, consider the multiplication of algebraic expressions. When multiplying two binomials, such as (x + 2) and (x - 3), the product is a quadratic expression: x² - x - 6. Here, the product not only represents a numerical value but an expression that encapsulates the relationship between variables.

In mathematics, products can also extend beyond numbers to include sets and functions. The Cartesian product, for instance, combines two sets to form a new set of ordered pairs. Similarly, the product of functions involves applying one function to the result of another, illustrating how the concept of a product transcends numerical operations to encompass broader mathematical structures.

Properties of Product

The product operation in mathematics is governed by several key properties that ensure consistency and reliability in calculations. These properties include:

• Commutative Property: The order of the numbers does not affect the product. For example, 3 × 4 equals 4 × 3, and both yield a product of 12.
• Associative Property: The grouping of the numbers does not affect the product. For instance, (2 × 3) × 4 is the same as 2 × (3 × 4), both resulting in a product of 24.
• Distributive Property: This property links multiplication and addition, allowing the product to be distributed over addition. For example, 5 × (2 + 3) equals (5 × 2) + (5 × 3), resulting in a product of 25.
• Identity Property: The product of any number and one is the number itself. For example, 7 × 1 equals 7.
• Zero Property: The product of any number and zero is zero. For example, 9 × 0 equals 0.

These properties are essential in simplifying mathematical expressions and solving equations. They provide a framework that mathematicians and students can rely on to ensure accurate and efficient calculations.

Types of Products in Mathematics

In mathematics, the term 'product' can refer to different types of results depending on the context. Some of the most common types of products include:

Read also:

Winning Big With New York Lotto Everything You Need To Know

Numerical Product

This is the most familiar type of product, resulting from the multiplication of numbers. It is the foundation of arithmetic and is used in everyday calculations.

Algebraic Product

In algebra, the product involves multiplying variables, constants, or expressions. The algebraic product can yield polynomials or other functions, which are fundamental to algebraic manipulation and equation solving.

Matrix Product

In linear algebra, the product of matrices involves a different rule set than numerical multiplication. The matrix product, also known as the matrix multiplication, is crucial for transforming data, solving systems of equations, and performing advanced mathematical operations.

Vector Product

Also known as the cross product, the vector product in vector calculus results in a vector perpendicular to the two input vectors. This type of product is significant in physics and engineering for calculating torque and rotational forces.

These types of products illustrate the versatility and adaptability of multiplication in mathematics, allowing it to be applied across various fields and disciplines.

How is Product Used in Math?

The product is used in various mathematical operations and applications, ranging from basic arithmetic to complex problem-solving. Some key uses include:

• Arithmetic Operations: The product is one of the four fundamental operations in arithmetic, essential for everyday calculations involving multiplication.
• Solving Algebraic Equations: Products are used to expand expressions, simplify equations, and solve for variables in algebra.
• Calculating Areas and Volumes: In geometry, the product of dimensions (length, width, height) is used to calculate the area of surfaces and the volume of solids.
• Statistical Analysis: Products are used in statistical computations, such as calculating probabilities and expected values.
• Graphical Transformations: In linear algebra, matrix products are used to perform transformations and rotations of graphical objects.
• Scientific Calculations: Products are used in physics, chemistry, and biology for calculating rates, forces, and other scientific measurements.

These applications demonstrate the product's integral role in both theoretical mathematics and practical problem-solving, highlighting its importance in various mathematical contexts.

Examples of Product in Mathematics

Understanding the concept of a product in mathematics can be enhanced through practical examples. Here are a few scenarios that illustrate the application of products:

Example 1: Basic Arithmetic

If you have 5 apples and you want to distribute them equally among 4 friends, you calculate the product: 5 × 4 = 20 apples. This example shows the use of a numerical product in everyday arithmetic.

Example 2: Algebraic Expression

Consider the multiplication of two binomials: (x + 3)(x - 2). The product is x² + x - 6. This example demonstrates the use of an algebraic product in simplifying expressions.

Example 3: Matrix Multiplication

Matrix A (2 × 3) and Matrix B (3 × 2) can be multiplied to produce a new matrix C (2 × 2). The elements of matrix C are derived from the products of corresponding elements in matrices A and B.

Example 4: Vector Cross Product

Given two vectors A = (1, 2, 3) and B = (4, 5, 6), the cross product A × B results in a new vector (-3, 6, -3), which is perpendicular to both A and B.

These examples illustrate the diverse applications of products in mathematics, from simple calculations to complex algebraic and geometric operations.

Importance of Product in Real Life

The concept of a product is not limited to theoretical mathematics; it plays a crucial role in various real-life scenarios, such as:

• Financial Calculations: Products are used to calculate interests, investments, and expenses in finance and economics.
• Engineering and Construction: Engineers use products to determine material requirements, structural integrity, and design specifications.
• Science and Research: In scientific research, products are used to calculate rates, concentrations, and other vital measurements.
• Technology and Computing: Computer scientists use products in algorithms, data processing, and graphical transformations.
• Everyday Life: From cooking recipes to shopping, products are used to determine quantities and measurements in daily activities.

The product's importance in these areas highlights its versatility and indispensability in both academic and practical contexts, making it an essential component of mathematical literacy.

Product in Algebra

In algebra, the product plays a pivotal role in manipulating and simplifying expressions, equations, and functions. Algebraic products are used in various operations, including:

• Expanding Binomials: The product of two binomials can be expanded using the distributive property to form a polynomial.
• Factoring Expressions: Finding the product of factors is critical in simplifying expressions and solving quadratic equations.
• Solving Systems of Equations: Products are used in methods like substitution and elimination to find solutions to simultaneous equations.
• Working with Polynomials: Algebraic products help in multiplying polynomials, finding roots, and determining the behavior of functions.

The product's role in algebra underscores its significance in understanding mathematical relationships and solving complex problems, making it an essential tool for students and mathematicians alike.

What Does Product Mean in Math Geometry?

In geometry, the concept of a product is instrumental in calculating various properties of shapes and figures. Some key applications of products in geometry include:

• Area Calculation: The product of length and width gives the area of a rectangle, while the product of base and height divided by two gives the area of a triangle.
• Volume Calculation: The product of length, width, and height determines the volume of a rectangular prism, while specific formulas apply to other shapes like cylinders and spheres.
• Scaling and Proportions: Products are used to scale geometric figures, maintaining their proportions and dimensions.
• Trigonometric Applications: In trigonometry, products are used to calculate angles, distances, and other properties of triangles.

The product's role in geometry highlights its importance in quantifying and understanding the spatial properties of shapes, contributing to a comprehensive understanding of geometric concepts.

Product in Calculus

In calculus, the product is a fundamental concept that aids in understanding the behavior of functions and their rates of change. Key applications include:

• Product Rule: In differentiation, the product rule is used to find the derivative of the product of two functions.
• Integration by Parts: This technique involves integrating the product of functions, breaking it down into simpler integrals.
• Applications in Physics: Calculus products are used to calculate work, energy, and other physical quantities involving rates of change.
• Analyzing Function Behavior: Products are used in analyzing the growth, decay, and behavior of functions over intervals.

The product's application in calculus underscores its significance in understanding dynamic systems and solving complex mathematical problems, making it an essential tool in higher mathematics.

Common Misconceptions About Product

Despite its fundamental nature, the concept of a product is often misunderstood. Some common misconceptions include:

• Product Always Means Multiplication: While the product typically involves multiplication, it can also refer to combined results in other contexts, such as Cartesian products and function compositions.
• Product is Only for Numbers: The product can apply to variables, expressions, matrices, vectors, and other mathematical entities.
• Product Properties Are Universal: While properties like commutativity and associativity apply to numbers, they may not hold for matrices and certain functions.
• Product is a Simple Operation: The product can become complex in advanced mathematics, requiring a deep understanding of underlying principles and methods.

Addressing these misconceptions is crucial for a clear and accurate understanding of the product and its applications across various mathematical domains.

Product in Computer Science

In computer science, the concept of a product is integral to various computational processes and algorithms. Key applications include:

• Data Processing: Products are used in data processing algorithms to perform calculations and transformations on data sets.
• Matrix Operations: Matrix products are used in computer graphics, machine learning, and simulations to perform transformations and calculations.
• Algorithm Design: Products are used in designing algorithms for sorting, searching, and optimizing processes.
• Cryptography: Products are used in cryptographic algorithms to secure data and communications.

The product's role in computer science highlights its importance in developing efficient and effective computational solutions, making it a vital component of modern technology.

Product in Economics and Business

In economics and business, the concept of a product is used to analyze and optimize production, sales, and financial strategies. Key applications include:

• Cost and Revenue Analysis: Products are used to calculate costs, revenues, and profits, aiding in financial decision-making.
• Production Optimization: The product is used to determine optimal production levels and resource allocation.
• Market Analysis: Products are used in market analysis to assess demand, supply, and competitive positioning.
• Investment Strategies: Products are used in calculating returns on investment and developing financial strategies.

The product's application in economics and business underscores its significance in understanding and optimizing economic activities, contributing to informed decision-making and strategic planning.

Historical Perspective of Product

The concept of a product has a rich history, evolving alongside the development of mathematics. Key historical milestones include:

• Ancient Civilizations: The Babylonians and Egyptians used products for trade and construction, laying the groundwork for modern arithmetic.
• Greek Mathematics: Greek mathematicians like Euclid formalized the concept of a product in geometry and number theory.
• Medieval Mathematics: Islamic mathematicians expanded on Greek concepts, developing algebraic products and advancing mathematical understanding.
• Renaissance Mathematics: The Renaissance saw the formalization of algebraic notation and the widespread application of products in solving equations.
• Modern Mathematics: The development of calculus, linear algebra, and other mathematical fields further expanded the application of products.

This historical perspective highlights the product's enduring significance in mathematics, reflecting its evolution and adaptation to meet the needs of various mathematical disciplines and applications.

Frequently Asked Questions

What is the product of two numbers?

The product of two numbers is the result obtained by multiplying them together. For example, the product of 3 and 4 is 12.

How is the product different from a sum?

The product refers to the result of multiplication, while the sum refers to the result of addition. They are distinct operations with different properties and applications.

Can the product be a negative number?

Yes, the product can be negative if one or both of the numbers being multiplied are negative. For example, the product of -3 and 4 is -12.

What is the product rule in calculus?

The product rule in calculus is a formula used to find the derivative of the product of two functions. It states that the derivative of a product is the derivative of the first function times the second function, plus the first function times the derivative of the second function.

How do you find the product of matrices?

The product of matrices is found by multiplying the rows of the first matrix by the columns of the second matrix and summing the products. The resulting matrix has dimensions based on the number of rows in the first matrix and the number of columns in the second matrix.

Why is the product important in mathematics?

The product is important in mathematics because it is a fundamental operation used in various mathematical calculations and applications, from basic arithmetic to advanced calculus and algebra.

Conclusion

The concept of a product in mathematics is a cornerstone of numerical operations and theoretical exploration. Its applications span arithmetic, algebra, geometry, calculus, and beyond, illustrating its versatility and indispensability. By understanding the product's properties, types, and uses, individuals can enhance their mathematical literacy and problem-solving skills, paving the way for success in academic and practical endeavors. The product's role in real-world applications further underscores its importance, making it a vital component of everyday life and professional fields. As mathematics continues to evolve, the concept of a product will remain a fundamental element, bridging the gap between numbers and their infinite possibilities.