Mastering Math Symbols: Greater Than And Less Than Sign In Focus

The "greater than" and "less than" signs are more than just mathematical symbols; they're fundamental tools that aid in understanding relationships between numbers. Their usage extends beyond basic mathematics into fields like science, engineering, and even everyday decision-making. Mastering these signs not only helps in solving mathematical problems but also sharpens logical reasoning and analytical skills. This article will delve into the intricacies of these symbols, exploring their history, applications, and significance in both academic and real-world contexts.

At first glance, the greater than (>) and less than (

This comprehensive guide will provide a detailed examination of the greater than and less than signs, offering insights into their history, teaching methods, and practical applications. We will also address common misconceptions and provide tips for overcoming challenges associated with these symbols. Through this exploration, readers will gain a deeper appreciation for these indispensable tools, equipping them with the knowledge needed to apply these concepts confidently in various contexts.

Read also:

Winning Big With New York Lotto Everything You Need To Know

Table of Contents

• History of Greater Than and Less Than Signs
• Why Are Greater Than and Less Than Signs Important?
• Real-World Applications of Greater Than and Less Than Signs
• Teaching Greater Than and Less Than Signs to Students
• What Do Greater Than and Less Than Symbols Look Like?
• Common Errors with Greater Than and Less Than Signs
• How Are Greater Than and Less Than Used in Mathematics?
• Understanding Inequalities: Greater Than and Less Than
• Using Visual Aids to Teach Greater Than and Less Than
• How Technology Enhances Learning of Greater Than and Less Than?
• Overcoming Challenges with Greater Than and Less Than Signs
• Interactive Learning Techniques for Greater Than and Less Than
• Assessing Understanding of Greater Than and Less Than
• Impact of Greater Than and Less Than Signs on Career Choices
• FAQs
• Conclusion

History of Greater Than and Less Than Signs

The greater than (>) and less than (

Before the introduction of these symbols, mathematicians used verbose language or different symbols to convey the idea of comparing quantities. Harriot's innovation provided a standardized way to represent inequality, which has since become an integral part of mathematical language. The adoption of these symbols marked a significant advancement in mathematical communication, facilitating the expression of complex ideas with brevity and precision.

Over time, the greater than and less than signs have become universal symbols used in mathematics education worldwide. Their simplicity and efficiency make them ideal for teaching students the concept of comparison from an early age. As mathematics evolved, these symbols found their place in various mathematical disciplines, including algebra, calculus, statistics, and more, showcasing their versatility and enduring relevance.

Why Are Greater Than and Less Than Signs Important?

Greater than and less than signs are essential in mathematics for several reasons:

• They provide a means to compare numbers and quantities, helping students develop a sense of numerical order and magnitude.
• These symbols are crucial for solving inequalities, a fundamental concept in algebra and calculus.
• They aid in data analysis, allowing for the comparison of statistical data and trends.
• Greater than and less than signs simplify mathematical expressions and equations, making them easier to interpret and solve.

Beyond mathematics, greater than and less than signs play a significant role in decision-making processes. In fields such as economics, finance, and engineering, these symbols are used to compare variables, optimize processes, and make informed choices. Their application extends to everyday life as well, where individuals use these symbols, often unconsciously, to compare prices, distances, and other quantities.

In summary, greater than and less than signs are versatile tools that enhance mathematical understanding and problem-solving skills. Their importance lies in their ability to convey complex ideas with simplicity and precision, making them indispensable in both academic and practical contexts.

Read also:

Mastering Jupyter Notebook Your Ultimate Guide To Interactive Computing

Real-World Applications of Greater Than and Less Than Signs

The utility of greater than and less than signs extends far beyond the classroom. These symbols are employed in various real-world scenarios, including:

Economics and Finance

In economics, greater than and less than signs are used to compare economic indicators, such as GDP growth rates, inflation rates, and interest rates. These comparisons help economists assess economic performance and make predictions about future trends.

In finance, these symbols are used to compare investment returns, analyze risk-reward ratios, and optimize portfolio allocations. Investors rely on these comparisons to make informed decisions about asset allocation and risk management.

Science and Engineering

Scientists use greater than and less than signs to compare experimental results, determine statistical significance, and analyze data trends. In engineering, these symbols are used to compare measurements, assess tolerances, and optimize design parameters.

For example, in quality control, engineers use these symbols to determine whether a product meets specified tolerances. In research, scientists use these symbols to compare variables and assess the significance of experimental results.

Everyday Life

Greater than and less than signs are commonly used in everyday life to compare prices, distances, quantities, and more. Whether shopping for groceries, planning a trip, or analyzing personal finances, these symbols help individuals make informed decisions.

For instance, when comparing prices at a store, individuals use these symbols to determine the better deal. When planning a trip, these symbols are used to compare distances, travel times, and costs to choose the most efficient and cost-effective option.

Teaching Greater Than and Less Than Signs to Students

Teaching greater than and less than signs to students is fundamental in building their mathematical foundation. This process involves several key strategies:

Introduction to Symbols

Begin by introducing students to the greater than (>) and less than (

Interactive Exercises

Engage students in interactive exercises that involve comparing numbers and quantities using greater than and less than signs. Use manipulatives, such as number cards or counters, to provide hands-on practice and reinforce understanding.

Real-World Examples

Incorporate real-world examples into lessons to demonstrate the practical applications of greater than and less than signs. Use scenarios that students can relate to, such as comparing the prices of items at a store or the distances between two locations.

Visual Aids

Utilize visual aids, such as diagrams, charts, and number lines, to help students visualize the concept of comparison. These tools can enhance understanding and make abstract concepts more concrete.

Assessment and Feedback

Assess students' understanding through quizzes, tests, and practical exercises. Provide feedback to help students identify areas for improvement and reinforce their learning. Encourage students to ask questions and seek clarification to deepen their understanding.

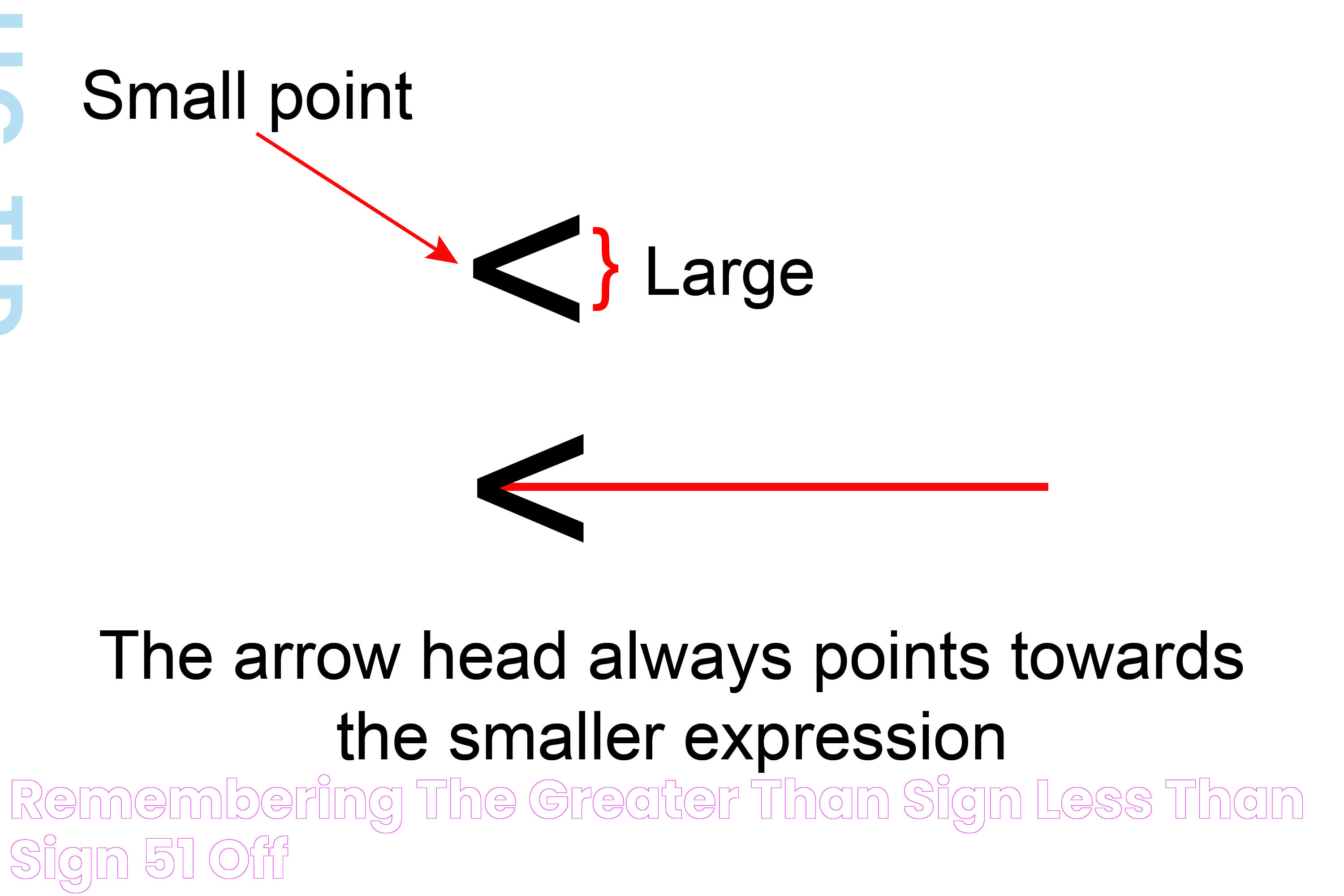
What Do Greater Than and Less Than Symbols Look Like?

The greater than (>) and less than (

The greater than (>) symbol is used to indicate that the quantity on the left is larger than the quantity on the right. For example, in the expression "5 > 3," the greater than symbol shows that 5 is larger than 3.

The less than (

These symbols are typically placed between two numbers or expressions, clearly indicating the relationship between them. Their simplicity and efficiency make them ideal for conveying the concept of comparison in a concise and easily understandable manner.

In addition to their basic usage, these symbols are also used in conjunction with other mathematical operations, such as addition, subtraction, multiplication, and division. They play a crucial role in solving inequalities, a fundamental concept in algebra and calculus.

Common Errors with Greater Than and Less Than Signs

Despite their simplicity, greater than and less than signs can sometimes lead to misunderstandings and errors. Here are some common mistakes and tips for avoiding them:

Reversing the Symbols

One common error is reversing the symbols, which can lead to incorrect conclusions. To avoid this mistake, remember the mnemonic "The alligator eats the bigger number," where the open side of the symbol faces the larger quantity.

Misplacing the Symbols

Another mistake is misplacing the symbols within an equation or expression. Ensure that the symbols are placed correctly to accurately convey the intended relationship.

Overlooking Negative Numbers

When comparing negative numbers, remember that the number closer to zero is greater. For example, -3 is greater than -5, even though the absolute value of 5 is larger. Pay attention to the context and consider the signs of the numbers involved.

Ignoring Context

Sometimes, students may overlook the context of a problem, leading to incorrect interpretations. Always consider the context and ensure that the symbols are used appropriately to convey the intended meaning.

Practicing with Examples

To reinforce understanding and avoid errors, practice using greater than and less than signs with a variety of examples. Use real-world scenarios and mathematical problems to apply these symbols in different contexts.

How Are Greater Than and Less Than Used in Mathematics?

Greater than and less than signs are integral to various mathematical concepts and operations. Their usage extends beyond simple comparisons, playing a crucial role in equations, inequalities, and more:

Comparing Numbers

The primary use of greater than and less than signs is to compare numbers and quantities. These comparisons help students develop a sense of numerical order and magnitude, laying the foundation for more advanced mathematical concepts.

Solving Inequalities

Inequalities are mathematical statements that involve greater than or less than signs. They represent a range of possible solutions rather than a single value, making them essential in algebra and calculus.

For example, the inequality "x > 3" indicates that the variable x can take any value greater than 3. Solving inequalities involves finding the set of values that satisfy the given condition.

Graphing Inequalities

Graphing inequalities is a visual way to represent the solution set of an inequality. It involves shading the region on a number line or coordinate plane that satisfies the given condition. This technique helps students visualize the concept of inequalities and understand their solutions.

Using with Other Operations

Greater than and less than signs are often used in conjunction with other mathematical operations, such as addition, subtraction, multiplication, and division. These combinations are common in algebraic expressions and equations, where the symbols help convey the relationships between variables and constants.

Analyzing Data

In statistics, greater than and less than signs are used to compare data sets, analyze trends, and draw conclusions. These comparisons help statisticians identify patterns, make predictions, and assess the significance of their findings.

Understanding Inequalities: Greater Than and Less Than

Inequalities are a fundamental concept in mathematics that involve comparing two quantities or expressions using greater than and less than signs. They play a crucial role in algebra, calculus, and various other mathematical disciplines. Understanding inequalities is essential for solving a wide range of mathematical problems.

Types of Inequalities

There are several types of inequalities, each with its own characteristics and solutions:

• Strict Inequalities: These involve the greater than (>) or less than ( 3" means that x is greater than 3.
• Non-Strict Inequalities: These involve the greater than or equal to (≥) or less than or equal to (≤) symbols and indicate that the two sides may be equal. For example, "x ≤ 5" means that x is less than or equal to 5.

Solving Inequalities

Solving inequalities involves finding the range of values that satisfy the given condition. This process is similar to solving equations, with a few key differences:

• When multiplying or dividing both sides of an inequality by a negative number, the direction of the inequality sign must be reversed.
• Graphing the solution set on a number line or coordinate plane can help visualize the range of possible values.

Applications of Inequalities

Inequalities have numerous applications in mathematics and beyond:

• In algebra, inequalities are used to solve problems involving ranges and constraints.
• In calculus, inequalities help determine limits, continuity, and convergence.
• In optimization, inequalities are used to define constraints and find optimal solutions.
• In statistics, inequalities help assess the significance of data and draw conclusions.

Understanding inequalities and their applications is essential for developing advanced mathematical skills and solving complex problems. By mastering this concept, students can enhance their problem-solving abilities and apply mathematical reasoning to a wide range of real-world scenarios.

Using Visual Aids to Teach Greater Than and Less Than

Visual aids are powerful tools for teaching greater than and less than signs, as they help students understand and internalize abstract concepts. These aids provide a concrete representation of mathematical ideas, making them easier to grasp and remember. Here are some effective visual aids for teaching greater than and less than:

Number Lines

Number lines are a simple yet effective way to visualize the concept of comparison. By plotting numbers on a line, students can easily see which numbers are greater or less than others. This visual representation helps reinforce the idea of numerical order and magnitude.

Diagrams and Charts

Diagrams and charts can illustrate the relationship between numbers and quantities. For example, a bar chart can show the comparison between the heights of two objects, with the taller bar representing the greater quantity. These visual aids help students understand the concept of comparison in a visual and intuitive way.

Manipulatives

Manipulatives, such as counters, blocks, or number cards, provide hands-on practice and reinforce understanding. By physically manipulating objects, students can explore the concept of greater than and less than in a tangible way, enhancing their comprehension and retention.

Interactive Tools

Interactive tools, such as digital games and apps, engage students in interactive exercises that involve comparing numbers and quantities. These tools provide immediate feedback and can be customized to suit different learning levels, making them an effective way to reinforce understanding and practice skills.

Real-World Scenarios

Incorporating real-world scenarios into lessons helps students see the practical applications of greater than and less than signs. Use examples that students can relate to, such as comparing the prices of items at a store or the distances between two locations.

By using visual aids and interactive tools, teachers can create an engaging and effective learning environment that helps students master the concept of greater than and less than. These tools make abstract concepts more concrete and accessible, enhancing students' understanding and confidence in their mathematical abilities.

How Technology Enhances Learning of Greater Than and Less Than?

Technology has revolutionized the way students learn and understand mathematical concepts, including greater than and less than signs. By integrating technology into lessons, educators can enhance students' learning experiences and provide them with valuable tools for mastering these fundamental concepts.

Interactive Software and Apps

Interactive software and apps provide engaging exercises and activities that reinforce understanding of greater than and less than signs. These tools offer immediate feedback, allowing students to practice and improve their skills at their own pace. Many apps also include games and challenges that make learning fun and motivating.

Online Resources and Videos

Online resources and educational videos offer explanations, demonstrations, and examples of greater than and less than signs in action. These resources provide students with additional support and opportunities to explore concepts in depth. Videos can also illustrate real-world applications, helping students see the relevance of these symbols in everyday life.

Digital Manipulatives

Digital manipulatives, such as virtual number lines, counters, and blocks, provide hands-on practice in a digital format. These tools allow students to experiment with greater than and less than signs, exploring their relationships and applications in a visual and interactive way.

Online Assessment Tools

Online assessment tools provide teachers with valuable data on students' understanding and progress. These tools offer quizzes, tests, and interactive exercises that assess students' knowledge of greater than and less than signs. Teachers can use this data to identify areas for improvement and tailor their instruction to meet students' needs.

By leveraging technology, educators can create dynamic and engaging learning environments that help students master greater than and less than signs. Technology provides students with valuable tools and resources that enhance their understanding, motivation, and confidence in their mathematical abilities.

Overcoming Challenges with Greater Than and Less Than Signs

Despite their simplicity, greater than and less than signs can present challenges for some students. Overcoming these challenges is essential for building a strong mathematical foundation and developing problem-solving skills. Here are some strategies for addressing common difficulties with these symbols:

Clarifying Misconceptions

Address common misconceptions about greater than and less than signs by providing clear explanations and examples. Use relatable scenarios and visual aids to illustrate the concept of comparison, helping students understand the meaning and significance of these symbols.

Providing Practice and Reinforcement

Offer ample opportunities for practice and reinforcement to help students master greater than and less than signs. Use a variety of exercises, including hands-on activities, digital games, and real-world scenarios, to engage students and reinforce their understanding.

Encouraging Critical Thinking

Encourage students to think critically about the relationships between numbers and quantities. Ask open-ended questions that prompt students to explain their reasoning and justify their conclusions. This approach helps students develop a deeper understanding of the concept of comparison and its applications.

Offering Differentiated Instruction

Provide differentiated instruction to meet the diverse needs of students. Tailor lessons and activities to accommodate different learning styles, abilities, and interests. Use a variety of teaching methods, such as visual aids, interactive tools, and real-world examples, to engage and support all students.

Building Confidence and Motivation

Build students' confidence and motivation by celebrating their successes and progress. Provide positive feedback and encouragement to help students develop a positive attitude toward learning and problem-solving. Foster a supportive and inclusive classroom environment where students feel comfortable asking questions and seeking help.

By addressing challenges and providing targeted support, educators can help students overcome difficulties with greater than and less than signs. These strategies promote a deeper understanding of mathematical concepts and build students' confidence in their abilities.

Interactive Learning Techniques for Greater Than and Less Than

Interactive learning techniques engage students in hands-on, experiential activities that promote active participation and deeper understanding of mathematical concepts, including greater than and less than signs. Here are some effective interactive learning techniques for teaching these symbols:

Collaborative Activities

Encourage students to work together on collaborative activities that involve comparing numbers and quantities. Group activities foster communication, teamwork, and critical thinking skills, allowing students to learn from one another and build a deeper understanding of greater than and less than signs.

Role-Playing Scenarios

Use role-playing scenarios to help students apply greater than and less than signs in real-world contexts. Create scenarios that involve decision-making, problem-solving, and comparison, allowing students to practice using these symbols in a relatable and engaging way.

Interactive Games

Incorporate interactive games that reinforce understanding of greater than and less than signs. These games provide immediate feedback and motivation, making learning fun and engaging. Use digital games, board games, or card games that involve comparing numbers and quantities.

Problem-Based Learning

Use problem-based learning to engage students in complex, real-world problems that require the application of greater than and less than signs. Encourage students to explore different solutions, analyze data, and draw conclusions based on their understanding of comparison and inequality.

Project-Based Learning

Incorporate project-based learning to provide students with opportunities to explore greater than and less than signs in depth. Assign projects that involve research, data collection, and analysis, allowing students to demonstrate their understanding of these symbols and their applications.

By using interactive learning techniques, educators can create engaging and dynamic learning environments that help students master greater than and less than signs. These techniques promote active participation, critical thinking, and problem-solving skills, enhancing students' understanding and confidence in their mathematical abilities.

Assessing Understanding of Greater Than and Less Than

Assessing students' understanding of greater than and less than signs is essential for identifying areas for improvement and providing targeted support. Effective assessment strategies help educators gauge students' knowledge and skills, ensuring that they have a solid foundation in mathematical concepts. Here are some strategies for assessing understanding of greater than and less than:

Quizzes and Tests

Use quizzes and tests to assess students' knowledge of greater than and less than signs. Include a variety of question types, such as multiple-choice, short-answer, and problem-solving questions, to evaluate students' understanding and application of these symbols.

Practical Exercises

Incorporate practical exercises that involve comparing numbers and quantities using greater than and less than signs. Use real-world scenarios and hands-on activities to assess students' ability to apply these symbols in different contexts.

Observations and Checklists

Observe students' participation in classroom activities and use checklists to assess their understanding of greater than and less than signs. Look for evidence of students' ability to compare numbers, use symbols correctly, and explain their reasoning.

Student Self-Assessment

Encourage students to assess their own understanding of greater than and less than signs. Use reflection activities, such as journals or exit tickets, to prompt students to evaluate their knowledge and identify areas for improvement.

Feedback and Conferencing

Provide feedback and hold conferences with students to discuss their understanding of greater than and less than signs. Use this opportunity to address misconceptions, provide targeted support, and set goals for improvement.

By using a variety of assessment strategies, educators can gain valuable insights into students' understanding of greater than and less than signs. These strategies help identify areas for improvement, guide instruction, and support students' learning and development.

Impact of Greater Than and Less Than Signs on Career Choices

The understanding and application of greater than and less than signs have a significant impact on career choices, as these symbols are essential tools in various fields and industries. Mastery of these signs is crucial for success in careers that involve mathematics, data analysis, and decision-making. Here are some ways in which greater than and less than signs impact career choices:

Mathematics and Education

In mathematics and education, greater than and less than signs are fundamental concepts that are taught from an early age. Educators who understand these symbols can effectively teach students the importance of comparison and inequality, laying the foundation for advanced mathematical skills.

Science and Engineering

In science and engineering, greater than and less than signs are used to compare measurements, analyze data, and optimize processes. Professionals in these fields rely on these symbols to make informed decisions, assess tolerances, and determine the significance of experimental results.

Economics and Finance

In economics and finance, greater than and less than signs are used to compare economic indicators, analyze investment returns, and optimize portfolio allocations. Professionals in these fields use these symbols to make informed decisions and assess the potential risks and rewards of different options.

Data Analysis and Statistics

In data analysis and statistics, greater than and less than signs are used to compare data sets, analyze trends, and draw conclusions. Professionals in these fields rely on these symbols to identify patterns, make predictions, and assess the significance of their findings.

Everyday Decision-Making

In everyday life, greater than and less than signs are used to compare prices, distances, and quantities. This understanding is essential for making informed decisions and optimizing personal finances, travel plans, and other aspects of daily life.

Understanding greater than and less than signs is crucial for success in various career paths and industries. Mastery of these symbols enhances problem-solving skills, logical reasoning, and decision-making abilities, making them indispensable tools in both academic and professional contexts.

FAQs

What is the history of the greater than and less than signs?

The greater than (>) and less than (

How can I teach greater than and less than signs effectively?

Teaching greater than and less than signs effectively involves using a variety of strategies, such as visual aids, interactive exercises, real-world examples, and technology. These methods engage students and reinforce their understanding of the concept of comparison.

What are common errors with greater than and less than signs?

Common errors with greater than and less than signs include reversing the symbols, misplacing them within expressions, overlooking negative numbers, and ignoring context. To avoid these errors, provide clear explanations and ample practice opportunities.

What are the applications of greater than and less than signs in real life?

Greater than and less than signs have numerous applications in real life, including comparing prices, distances, and quantities. They are also used in fields such as economics, finance, science, engineering, and data analysis to compare variables and make informed decisions.

How do greater than and less than signs impact career choices?

Mastery of greater than and less than signs is crucial for success in careers that involve mathematics, data analysis, and decision-making. These symbols are essential tools in fields such as education, science, engineering, economics, finance, and statistics.

What are some effective interactive learning techniques for teaching greater than and less than signs?

Effective interactive learning techniques for teaching greater than and less than signs include collaborative activities, role-playing scenarios, interactive games, problem-based learning, and project-based learning. These methods engage students and promote active participation.

Conclusion

In conclusion, the greater than and less than signs are fundamental tools in mathematics, providing a means to compare numbers and quantities. Their simplicity and efficiency make them indispensable in both academic and real-world contexts. Understanding these symbols enhances mathematical literacy, problem-solving skills, and logical reasoning, laying the foundation for success in various fields and industries.

By exploring the history, applications, and teaching methods of greater than and less than signs, this article has highlighted their significance and versatility. Whether used in mathematics education, scientific research, or everyday decision-making, these symbols play a crucial role in simplifying and interpreting numerical data.

As we continue to advance in our understanding of mathematics and its applications, the greater than and less than signs will remain essential tools for communicating complex ideas with clarity and precision. By mastering these symbols, individuals can enhance their analytical skills and confidently apply mathematical concepts in diverse contexts.